ICAP-2002 Abstracts and Posters

The essence of collective simulations of the beam-beam interaction in particle colliders is (1) the propagation of the particles in two counter rotating bunches between adjacent interaction points through external fields and (2) the computation of the collective electromagnetic forces that the particles in one bunch exert on each of the particles of the other bunch, localized at the interaction points. The first part is straight forward and can be naively parallelized by assigning subsets of particles to different processors, and propagating them separately. The second part encompasses the core computational challenge which entails the summation of the collective effects of the particles in one beam on the individual particles in the other beam. 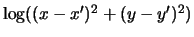Typically, for high energy colliders the computation of the collective forces is reduced to a 2 dimensional Poisson problem with Green's function proportional to $\log((x-x')^2+(y-y')^2)$ [1]. If there are

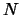
particles in each beam, a brute force calculation involves

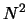
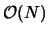
computations. For moderate size N, this can quickly becomes a prohibitively expensive operation. Fast Multipole Methods (FMM) are often invoked to reduce the number of calculations to ${\mathcal{O}}(N)$ [2,1]. Thus, current parallel implementations of FMM are inadequate for such simulations. In this work we describe a very simple parallelization of a FMM based beam-beam interaction code. We continue to use a serial FMM algorithm, but imbed it in a clever parallel communication scheme called Force Decomposition (FD) [4], initially developed for molecular dynamics simulations. Without the FMM, each processor in the FD algorithm would perform an

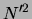
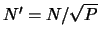
brute force calculation, where $N' = N/\sqrt{P}$ , where

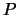
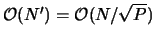
is the total number of processors used. By replacing this brute force computation with a serial FMM algorithm on each processor we reduce the computational complexity to ${\mathcal{O}}(N') = {\mathcal{O}}(N/\sqrt{P})$ .

The advantage of this combined FMM/FD parallel method is that is extremely easy to implement. The FD method itself involves only three calls to MPI routines, and core FMM calculations are performed exactly as in a serial based FMM code, just now on a reduced set of sources and target particles. We demonstrate the speedup of 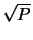$\sqrt{P}$ of our parallel code over a serial code and indicate directions for future work to increase the order of this speedup.

References

[1] M.Vogt, T.Sen, J.A.Ellison, Simulations of Three 1-D Limits of the Strong-Strong Beam-Beam Interaction in Hadron Colliders Using Weighted Macro-Particle Tracking Phys. Rev. ST Accel. Beams 5, 024401 (2002) and FNAL Pub-01/096-T (2001); M.Vogt, J.A.Ellison, T.Sen, R.L.Warnock, Two Methods for Simulating the Strong-Strong Beam-Beam Interaction in Hadron Colliders, Proc. Beam-Beam Workshop at Fermilab (2001);

[2] L. Greengard, L Rokhlin, A Fast Algorithm For Particle Simulations, Journal of Computational Physics 73, 325-348 1987.

[3] M.S. Warren and J.K. Salmon, A Portable Parallel Particle Program Computer Physics Communication 87, 266-290 (1995);

J.K. Salmon, M.S. Warren, and G.S. Winckelmans, Fast Parallel Tree Codes for Graviational and Fluid Dynamical N-Body Problems, International Journal of Supercomputer Applications and High Performance Computing 8, 129-142 (1994).

[4] S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comp Phys. 117, 1 (1995); B. Hendrickson and S. Plimpton Parallel Many-Body Simulatins Without All-to-All Communications,Journal of Parallel and Distributed Computing, 27, 15-25 (1995); Alsing, P.M., Kale, R.P., and Fleharty, M.E., Parallel Molecular Dynamics Visualization using MPI and MPE Graphics, Proceedings IEEE, Second MPI Developers Conference, Library of Congress #96-76653, 104 (July 1-2, 1996).

Paul M. Alsing, Vinay Boocha, Mathias Vogtm, James Ellison

Go Back to the ICAP02 Talks Schedule page.
Go Back to the ICAP02 Posters page.
Go Back to the ICAP02 home.

This page is maintained by Kyoko Makino.